یکی از برجسته‌ترین کاربردهای عملی کامپیوترِ کوانتومی شبیه‌سازی سیستم‌های کوانتومی دیگر است. تاکنون، تنها برای سیستم‌های کوانتومی بسته یعنی سیستم‌های که با محیط اطراف برهم کنش ندارند، امکان شبیه سازی دقیق وجود داشت. اما مارتین کلیچ و همکارانش از دانشگاه فری برلین و دانشگاه پتسدام در آلمان[1]  در مجله فیزیکال ریویو لِتِرز[2]، نشان دادند که سیستم‌های بازِ کوانتومی که با محیط اطرافشان برهمکنش دارند را نیز می‌توان به خوبی با کامپیوترهای کوانتومی شبیه سازی کرد. و دریچه‌ای تازه به سوی کاربردهای مهم کامپیوتر‌های کوانتومی در فیزیک ماده چگال، شیمی کوانتومی، و حتی زیست‌شناسی گشودند.

شبیه‌سازی سیستم‌های بس ذره‌ای کوانتومی کار دشواریست. شناخته‌شده‌ترین الگوریتم‌ها برای شبیه‌سازی دقیق سیستم‌های بس‌ذره‌ای کوانتومی با بر همکنش‌های زیاد، در کامپیوتر کلاسیکی نیازمند منابع محاسباتی‌ی است که با تعداد ذرات بصورت نمایی رشد کنند. این مقیاس‌گذاری نامناسب، شبیه سازی دقیق پدیده های مهمی مانند اَبر رسانایی در دمای بالا را که شامل تعداد زیادی ذره هستند، از دستیابی محاسباتی ما خارج می‌کند.

ریچارد فاینمن از نخستین کسانی بود که اشاره کرد که ممکن است این اشکال یک ویژگی سیستم‌های کوانتومی باشد. ممکن است که سیستم‌های کوانتومی در ماشین‌های کلاسیکی به دشواری شبیه سازی شوند، اما احتمالا می‌توانند به خوبی یکدیگر را شبیه سازی کنند. ایده فاینمن توسط دیوید دوچ[3] پیش‌برده‌شد، او نشان داد که می‌توان یک مدل محاسباتی کاملا کوانتومی تعریف کرد و  نشان داد که چگونه ایده های شبیه سازی فاینمن عملی می‌شوند.

در کامپیوتر کوانتومی، ورودی های بهم پیوسته‌ی منطقی بیت‌های کوانتومی یا کیوبیت‌ها[4] را ثبت می‌کنند. این ورودی‌ها یکانی هستند، یعنی حالت‌های کوانتومی به شکل پیوسته و برگشت‌پذیر دگرگون می‌شوند. گمان می‌شود که توان محاسباتی کامپیوتر‌های کوانتومی بیش از کامپیوترهای کلاسیکی است. زیرا در کامپیوتر‌های کلاسیکی مشکلاتی وجود دارد که مشهورترینش فاکتور‌گیری اعداد صحیح است، که در کامپیوترهای کوانتومی بخوبی حل می‌شود. پژوهش‌های با شدت بیشتر در سراسر دنیا در جریان است تا روش‌های فیزیکی کامپیوتر‌‌های کوانتومی را برای کاربردی شدن در اندازه های مهم مقیاس‌پذیر کنند.

با این وجود تاکنون تحلیل‌های طرح شبیه سازی کوانتومی به شدت به سیستم های کوانتومی بسته محدود شده‌‌اند، نه سیستم‌های بازی که موقعیت‌های حقیقی زیادی را توصیف می‌کنند. سیستمی را بسته می‌نامیم که هیچ بر هم کنشی با سیستم های اطراف خود نداشته باشد. سیستم های بسته منزوی و جدا شده از دنیا هستند. بر طبق معادله شرودینگر که بیان می‌کند جزئیات فیزیکی یک سیستم در هامیلتونی آن نهفته است و جزئیات انرژی و برهم کنش‌های سیستم در عملگر ثبت می‌شود، این سیستم ها در زمان بصورت یکانی پیش می‌روند.

مطالعه سیستم های بسته نقش اساسی در فیزیک کوانتومی بازی می‌کند، و ما می‌توانیم بسیاری از اثرات مهم را به این شیوه مدل کنیم. هرچند سیستم هایی که ما در طبیعت می‌بینیم هرگز بسته نیستند. آنها با ذرات اطرافشان برهم کنش دارند و در بسیاری از موارد، رفتار فیزیکی آنها بر اساس همین برهم کنش ها تعیین می‌شود.

معادله شرودینگر برای توصیف سیستم های کوانتومیِ باز کافی نیست: روش‌های تازه ای لازم است. البته به دلایل زیادی مهم‌ترین این روشها معادله مَستر لویلیان[5] است، که می‌توان به عنوان جایگزینِ معادله شرودینگر در سیستم های کوانتومیِ باز، در نظر گرفت. لویلیان عملگریست که نقشی همانند هامیلتونی دارد، بر همکنش‌ها را مشخص می‌کند اما بیانگر فرآیند های اتلاف و پیوستگی ناشی از محیط اطراف نیز هست.

اگرچه شبیه سازی کوانتومی یکی از کاربردهای اولیه ای بود که برای کامپیوتر های کوانتومی پیشنهاد شد،  جزئیات آن تا پیش از نیمه ی دهه نود یعنی زمانی که سث لیوید[6] یک سری روش هایی را برای انجام ان ارائه کرد، مشخص نبود. در بسیاری از سیستم‌های که ما علاقه‌مند به شبیه‌سازی‌شان هستیم، همه مولفه‌ها بطور همزمان با هم بر همکنش دارند. یک کامپیوتر کوانتومی واقعی اما تنها در ورودی‌های گسسته کوانتومی و تنها روی چند کیوبیت بطور همزمان عمل می‌کند. لیوید معتقد بود که دینامیک پیچیده یک سیستم بس ذره ای برهمکنشی می‌تواند به بخش‌های ساده‌تری شکسته شود، که هر کدام تنها شامل برهم‌کنش‌های دو تایی بوده و بطور مستقیم با ورودی‌های یکانی کامپیوتر کوانتومی قابل شبیه سازی شدن هستند. ابزار ریاضیاتی که او برای نشان دادن این مساله بکار برد سوزوکی- تروتر[7] نام دارد.

قضیه سوزوکی- تروتر یک نتیجه ریاضیاتی در مورد تبدیلات یکانی است. بطوریکه می‌تواند در دینامیک سیستم‌های بسته کوانتومی بکار برده شود، زیرا این سیستم ها یکانی هستند. این نظریه بیان می‌کند که در شبیه سازی سیستم بس ذره ایِ بسته با بر هم کنش‌های دو به دو، می‌توان بر روی هر کدام از برهم کنش‌ها سویچ کرد، سویچ سریع استروبوسکوپی بین بر هم کنش‌های مجزا. هر قدر سویچ کردن استروبوسکوپی سریعتر باشد، تفریب بهتر خواهد بود و در حد سویچ با سرعت نا‌متناهی، دینامیک اصلی بطور کامل باز سازی می‌شود.

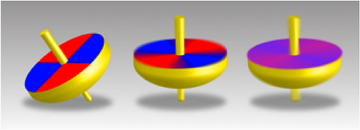
این اثر بسیار شبیه به یک حیله مشهور نوری است. اگر بالای یک فرفره را بصورت تکه های آبی و قرمز نقاشی کنیم و با سرعت بچرخانیم، رنگ‌های مجزا در هم می‌روند و بنابراین ما سایه ای بنقش می‌بینیم هرچند که هیچ قستمی از فرفره بنفش نیست.

کلیش و دوستانش نشان دادند که نظریه سوزوکی– تروتر را می‌توان به دینامیک سیستم‌های باز کوانتومی هم تعمیم داد. آنها نشان دادن که حیله استروبوسکوپیک برای دینامیک‌های لویلیان هم موثر است و قادر به بدست آوردن دقیق خطا در تقریب است. این نتایج نشان می‌دهند که سیستم های کوانتومی باز را می‌توان بخوبی با یک کامپیوتر کوانتومی شبیه سازی کرد. حالا حتی فعالیت‌های پژوهشی بیشتری مانند فیزیک مزوسکوپی، سنتز نوری، و شیمی کوانتومی غیر حرارتی را می‌توان به لیست زمینه‌های علمی اضافه کرد که کامپیوتر‌ِ کوانتومی برای‌شان نقش یک ابزار انقلابی را دارد.

منبع: http://physics.aps.org/articles/v4/72?referer=rss